Have you ever thought on why can't we leave earth's surface ? Why do we keep our feet always touching on the earth's surface ? Why can't we fly in the sky just as birds do ? Obviously, you would say, 'Because I don't have wings to fly'.
Having wings is not just a reason that birds can fly. It is because wings can do work against the pulling of earth's gravity. More the surface of wings, more it can produce energy against the gravity, the more it takes birds higher in the sky. But gravity does not stop pulling birds down to the earth's surface. After flying some times, birds get tired. They take benefit of branches of tree to take a rest. This is the magic of gravity of earth. It keeps pulling you. It does not want you go away from it.
It keeps saying you,
Love me like you do, la la love me like you do ....
Touch me like you do, ta ta touch me like do ...... (just a part of a song 😊).
And you need to keep touching it. You can't go away from it.
You might have been thinking, does only earth pulls us towards it ? Do or don't we pull it towards us ?
Here is the answer: Yes, we are also pulling the earth towards us. However, gravity of our bodies is so smaller that it is negligible as compared to earth's gravity. It is because our mass is very small as compared to earth's mass.
So, gravity is nothing but the force of pulling. Gravity due to body means the force with which it pulls other bodies towards it. And this force depends on both the body that is pulling and the body being pulled. The gravity always exists between two bodies. If one creates gravity there most be another body to experience effect of gravity. Otherwise, existence of that body and its gravity does not have any meanings. This might be the reason behind the planets to experience gravity of the sun, the moon on experience the earth's gravity. And of course, we also have the experience of earth's gravity. Earth's gravity is the reason of our existence on earth. So, let's be familiar with gravity and gravitational force.
In this post, we will learn things as listed below:
1. Gravitational Force
2. Acceleration due to gravity of planet
3. Escape Velocity
4. Expression for Escape Velocity
5. Escape Velocity due to Earth
6. Significance of escape of velocity
1. Gravitational Force: Newton's law of Gravitation
Sir Isaac Newton, in 1687, discovered the existence of force between two masses. The force between two masses is called gravitational force. The gravitational force is always attractive. This means that the masses attract each other by gravitational force. For example, the force between the earth and the moon.
According to Newton, every body in this universe attracts every other body with the force such that
- the force is directly proportional to the product of their masses
- the force is inversely proportional to the square of the distance between them.
The force is directed along the line joining the bodies.
If M and m are masses of two bodies separated with the distance d. Then
`F propto M m`---(1) and
`F propto \frac{1}{d^2}` -----(2)
Combining (1) and (2), we get
`F propto \frac{Mm}{d^2}`
`\rightarrow` `F = k \frac{Mm}{d^2}` ----(3)
Here `k` is a proportionality constant, called the universal gravitational constant. It is denoted by G and has value of `k = G = 6.67 \times 10^{-11} Nm^2kg^-2`. Thus equation (3) can be written as
`F = \frac{GMm}{d^2}` ------(4)
This equation represents the gravitational force between two bodies of masses M and `m` separated with the distance d.
Note:
The distance d is taken as the length of line joining the centers of two masses M and m. If the mass bodies just touch each other, then distance between them is the sum of their respective radius.
Suppose,
`M = 12 \times 10^6` kg
`m = 6 \times 10^5` kg
`d = 150 \times 10^9` m
Then from (4), we get
`F = \frac{6.67 \times 10^{-11} Nm^2kg^{-2} \times 12 \times 10^6 kg \times 6 \times 10^5 kg}{(150\times10^9 m)^2}`
`F = \frac{480.24 \times 10^{-11+6+5} Nm^2}{22500 \times 10^18 m^2}`
`F = \frac{480.24 \times 10^0 Nm^2}{22500 \times 10^18 m^2}`
`F = \frac{480.24 N}{22500 \times 10^18 m^2}`
`F = \frac{2.13 \times 10^{-2}N}{10^18} `
`F = 2.13 \times 10^{-20} N`
Thus, the gravitational force between these two bodies for given masses and separation is `2.13 \times 10^{-20} N`. This is very small value. It shows that gravitational force is very weak force. However, this force is still sufficient to hold these in their gravitational effect.
2. Acceleration due to gravity of planet
Acceleration due to a planet is the gravitational force experienced by a unit mass body. This means that if the gravitational force between two bodies is divided by mass of one of the body, then it is called acceleration due to the body experienced by the body whose mass is used to divide the gravitational force.
From equation (4), we have the gravitational force is given by
`F = \frac{GMm}{d^2}`
Then the acceleration due to gravity of the body of mass M experienced by the body of mass m is given as
`\frac{F}{m} = \frac{GM}{d^2}`
If R be the radius of body of mass M and another body of mass m is on the surface of mass M, then `R = d`.
`\frac{F}{m} = \frac{GM}{R^2}`
`g = \frac{GM}{R^2}` -----(5)
Usually acceleration due to gravity is denoted by 'g'. Equation (5) represents the expression for acceleration due to gravity of a planet of mass M and radius R experienced by the smaller body of mass m, when the smaller body is just on surface of the planet. Equation (5) shows that acceleration due to gravity of planet depends only on the mass and radius of the planet. Heavier the planet, greater will be acceleration due to its gravity. It does not depends on the mass or radius of body who is experiencing the acceleration due to gravity of planet.
For Earth,
`M = 6.0 \times 10^{24}`kg
`R = 6.4 \times 10^6`m,
Then from (5), acceleration due to gravity of earth is given by
`g_e = \frac{6.67 \times 10^{-11} Nm^kg^{-2} \times 6.0 \times 10^{24} kg}{(6.4 \times 10^6 m)^2}`
`g_e = \frac{40.02 \times 10^{-11+24} Nm^2kg^{-1}}{40.96 \times 10^{12} m^2}`
`g_e = \frac{0.981 \times 10^{13} kgms^{-2}m^2kg^{-1}}{10^{12} m^2}`
`g_e = 0.981 \times 10 ms^{-2}`
`g_e = 9.81 ms^{-2}` -----(6)
Thus, this value of acceleration due to gravity of earth means that the velocity of smaller body freely falling towards the earth's surface increases with `9.81 ms^{-2}`.
3. Escape Velocity
When a body tries to go up from the surface of any planet, the body falls down due gravity of the planet. So, the body can't leave the surface of the planet. When the same body is thrown up in sky with some velocity, the body goes up. But its velocity starts to decrease due to the gravity of planet that pulls back the body. After reaching up to some height, the body falls down to the surface of planet. This happens until the thrown body reaches out of the region where the effect of gravity of planet does not exist.
From this region, the body escapes from effect of gravity and it never falls back to the surface of planet.
Thus, the velocity of body thrown up from the surface of a planet, which takes it out of the gravitational effect of the planet is called escape velocity. In other words, the escape velocity of a body is a minimum velocity with which the body needs to be projected upward so that the body just overcome the gravitational pull of the planet.
4. Expression for Escape Velocity
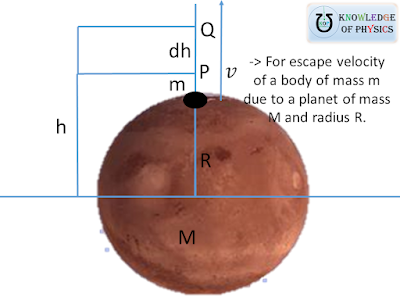
Let's consider a body of mass m projected with the velocity v from the planet of mass M and radius R. Then kinetic energy of the body is given as
`E_k = \frac{1}{2}mv^2` ----(i)
Fig.1 Showing a body of mass m projected with velocity `v`
from the surface of a planet of mass M and radius R.
To move the upward, it has to do the work against the gravity of the planet. The body uses its kinetic energy to do the work against the gravitational force on it.
After some time, let the body reaches to the point P at height h from the surface of planet from it was thrown up. When the body is at point P, the gravitational force between the body and the planet is given as
`F = \frac{GMm}{h^2}` ---(ii)
The body has to do the work against this force. From the point P, let the body moves up with small height dh, from P to Q, against the gravitational force given by (ii). Then work done against the gravity is given as
`dW = F \times (- dh)`
`\rightarrow` `dW = - \frac{GMm}{h^2} dh` ---(iii)
For the body to escape from the surface of the planet to out of the gravitational effect of the planet, we need to integrate equation (iii) with respect to the height from h = R to h = `\infty`. Thus, the total work done against the gravitational force is given as
`W = \int_R^{\infty} dW`
`\therefore`Learn more about integration from
HERE.
or, `W = - \int_R^{\infty} \frac{GMm}{h^2} dh`
or, `W = - GMm \int_R^{\infty} h^{-2}dh`
or, `W = -GMm [|frac{h^{-2+1}}{-2+1}]_R^{\infty}`
or, `W = - GMm [\frac{h^{-1}}{-1}]_R^{\infty}`
or, `W = GMm [\frac{1}{h}]_R^{\infty}`
or, `W = GMm [\frac{1}{\infty} - \frac{1}{R}]`
or, `W = GMm [0 - \frac{1}{R}]`
`\therefore` `W = - \frac{GMm}{R}` ---(iv)
This is the required expression for the work done of the body. The negative sign indicates that work needs to be done against the gravity. So, taking only positive value,
`\therefore` `W = \frac{GMm}{R}` ---(v)
Equation (v) shows that work done depends on masses of the planet and the body and the radius of the planet.
The energy for the work done needs to be supplied by the kinetic energy of the projected body. If `v_e` represents escape velocity of the body, then equation (i) can be written as
`E_k = \frac{1}{2}mv_e^2` --(vi)
For escaping of the body,
`E_k = W`
or, `\frac{1}{2} mv_e^2 = \frac{GMm}{R}`
or. `v_e^2 = \frac{2GMm}{mR^2}`
`\therefore``v_e = \sqrt{\frac{2GM}{R}}` ----(vii)
But `g = \frac{GM}{R^2}`, then
`v_e = \sqrt{\frac{2GM}{R}}`
or, `v_e = \sqrt{2\frac{GM}{R^2} \times R}`
or, `v_e = \sqrt{2 g R}`
`\therefore` `v_e = \sqrt{2gR}` -----(viii)
This equation represents the expression for the escape velocity of the body.
This expression shows that escape velocity depends on acceleration due to gravity of the planet and its radius. g depends on both mass M and radius R of the planet. So, heavier and larger the planet, higher will be the escape velocity.
5. Escape Velocity due to Earth
Escape velocity due to earth means the minimum velocity with which a body needs to be projected up in the sky so that it never comes back to the earth. We know, escape velocity due to earth depends on gravity and radius of earth.
For Earth,
`v_e = \sqrt{2g_e R_e}`
Using the values of earth
`g_e = 9.81 ms^{-2}` and
`R_e = 6.4 \times 10^6`m, we have
`v_e = \sqrt{2 \times 9.81 ms^{-2} \times 6.4 times 10^6 m}`
or, `v_e = \sqrt{125.568 \times 10^6 m^2s^{-2}}`
`v_e = 11.2057 \times 10^3 ms^{-1} `
`\therefore` `v_e = 11.2057 kms^{-1}` ----(ix)
This equation gives the value for the escape velocity due to the earth. This value of escape velocity suggests that if a body on earth surface is projected with a velocity of `11.2057 ms^{-1}`, the body escapes out of the earth's gravity. This means that this body never returns to the earth surface again. This value can be different for different planets because they have different mass, size and gravity.
6. Significance of Escape Velocity
Escape velocity is one of the parameters that determine the characteristics of planets. To learn more about characteristics of planets:
Click HERE.
High escape velocity means that the planet has high ability to hold other bodies under its gravitational field. High escape velocity means that the projected body needs to do more work against the gravity.
If the escape velocity due to a planet is high, it can hold all gas molecules in atmosphere within its gravitational field resulting thick layer of atmosphere.
For earth, escape velocity of a body is, `v_e = 11.2057 kms^{-1}`, which is a high value. This means that earth's gravitation can hold all gas molecules having velocity less than `11.2057 ms^{-1}` in its atmosphere. Almost no air particles can escape the earth gravity. This is one of the reasons that the earth has thick layer of atmosphere, suitable for both animal and plant breathings.
High surface temperature of the planet can enhance the average velocity of gas molecules. If the average velocity of a molecule exceeds the escape velocity. Then this molecule escapes from the planet's gravitation. Mercury, the closer planet from the sun, has high surface temperature. Since it is the smallest planet of Solar system, it has lower mass and lower radius. This results smaller gravity and smaller escape velocity. Due to high surface temperature, average velocity of gas molecules exceeds escape velocity. That is why Mercury does not have atmosphere. Similar is the case for the Moon, natural satellite of earth, as well. Thus, escape velocity due a planet plays significant role in holding the atmosphere in its sky.
Take me To Top





Comments
Post a Comment