common characteristics of planets of solar system | orbits and motion of planets | Knowledge of Physics

 The non-luminous bodies which revolve around the sun in fixed orbits without interfering the path and motion of each others are called the planets.

In this post, you will mainly learn about three things:

1. Common Characteristics of planets
2. Kepler's law of planetary motion
3. Atmosphere of planets.

There are 8 planets in solar system. They are obviously,

1. Mercury
2. Venus
3. Earth
4. Mars
5. Jupiter
6. Saturn 
7. Uranus
8. Neptune

Click Here to learn more about Solar System and its members.

Two Categories of Planets

1. Terrestrial Planet

The planets of this category are relatively small in size, have high density and made up of solid socks and metals. These are also called as Earth-like planets. These planets are Mercury, Venus, Earth and Mars.

2. Jovian Planet

The planets of this category are relatively large in size, have low density and made up of gases like hydrogen, helium, ammonia, methane etc. These planets are also referred as Jupiter-like planets. These are Jupiter, Saturn, Uranus and Neptune.

Common Characteristics of Planets:

i) All planets on solar system are non-luminous, this means neither of them has its own light. Some of them are visible because of the sun-light reflected by surface of these planets.

ii)  The terrestrial planets have smaller mass and size. But they have high density as compared to Jovian planets

iii) Except Mercury and Venus, all planets have at least one natural satellites, which revolve around them.

iv) All planets rotate in anti-clockwise direction, so that sun rises on them from East and sun sets in the west. But Venus and Uranus rotate in clockwise direction, that is, sun rises from west and sun sets from east.

v) All planets have at least thin layer of atmosphere. Atmosphere of these planets contains gases such as nitrogen, hydrogen, carbon dioxide, helium, oxygen, methane etc.

vi) All planets follow Kepler laws of planetary motion.

Kepler's Law of Planetary Motion:

1. First Law:

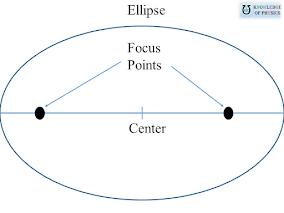
This tells us about the path of planets around the sun. According to first law, the planets move around the sun in elliptical path, called orbit, with the sun at one of foci of this elliptical path.

Fig.1 Shape of Ellipse and planet in elliptical orbit with sun at one of the focus points of ellipse.

2. Second Law:

This law tells us about area swept out and time taken by the planet in its orbit. According to this law, the radius, that is, the line joining the sun and the planet, sweeps out the equal area on equal time interval.

Fig.2 Motion of planet in orbit. 

Suppose, the planet is initially at point P and after t time it reaches to point Q, as shown in Fig.1. Then the area swept out by the radius or distance between sun and planet(OP) is OPQ. That is, OPQ = A

After few days, the planet passes nearby the sun and reaches at point P'. After same time interval t, let reaches to Q'. The area swept out by OP' is OP'Q'. Kepler's second law of planetary motion says that OPQ must be equal to OP'Q' for same time interval t. That is, OPQ = OP'Q' = A. 

3. Third Law:

 This law tells us about the relation of time of revolution of  planet with its distance from the sun. According to this law, the square of time of revolution of planet around the sun is directly proportional to its distance from the sun. That is,

`T^2 propto R^3`. 

Where, T = Time of revolution around the sun

R = radius of elliptical orbit or distance between sun and planet.

Atmosphere of Planets:

Mass and radius of the planet determines its gravity, that causes acceleration to freely falling body towards its surface. The presence and thickness of atmosphere on  a planet is determined by the value of acceleration due to gravity(g) of the planet and its surface temperature.

If  R be the radius of planet, then the escape velocity of a particle on the surface of the planet is,

`v_e = \sqrt{2gR}`

Learn more about Escape Velocity from HERE.

Similarly, if the absolute temperature of the surface of planet is T, then the average velocity of gas molecules at this temperature is given by

`v_{av} = \sqrt{\frac{3KT}{m}}`

where K is Boltzmann constant and m is mass of molecule.

When `v_{av}`of gas molecules is greater than escape velocity of the planet, then the gas molecules escape out from the gravitational field of the planet. This results the planet not to have atmosphere. 

For example,

 Surface temperature of Mercury is very high. So, the average velocity of gas molecules, if present here, is very high. However, Mercury is smaller in size and has very less mass. Thus average velocity of gas molecule is higher than escape velocity of the planet. Gas molecules escape out from the gravitational field of Mercury. So, Mercury does not have considerable atmosphere.

Jump to Top