Knowledge of Physics

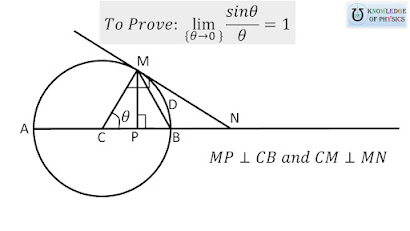
 In this post, you will learn to prove a very important formula in calculus,  `\lim_{\theta \rightarrow 0} \frac{sin \theta }{\theta} = 1`. This relation is very useful in determining the limit of trigonometric functions.  If you use `\theta = 0` directly in `\frac{sin \theta}{\theta}` then you get `\frac{0}{0}` which is an indeterminate form. This means that you can not find value of limit directly. However, if you use some techniques, then you get the limit equal to 1. In this post, you will learn that technique which helps you to find out the value of given limit easily.   Let's begin. Fig.1 Circle with center at C having radius CB = r and tangent MN at point M to prove the formula. Consider a circle ABDM with center at C and radius CB so that  CM = CB = AC = r. BDM  is an arc that subtends angle `\theta` at C.  MN is a tangent of circle at M that meets diameter AB extended at N so that CM is perpendicular to MN. Also, MP is drawn to perpendicular to CB at P.  Now we consider tw

Solving a mathematical problem is not an easy task. You need to have a lot of background knowledge to solve problems. If you a student of Physics, you need to solve many types of problem using mathematical relations. To be strong in Physics, you need to make yourself strong mathematics as well.   In this post, you will learn about the following topics:   What is equation ? What is trigonometric equation What the techniques or Steps of Solving Trigonometric equations? Problems with  Solutions of  different type of trigonometric equations Learn more about Trigonometric ratios and their formulae from HERE . 1. What is an Equation ? The mathematical relation of the form ax + bx + c = 0 which is true for certain values of given variable x, is called equation. For example, 2x+2 = 1 is an equation, which true only for `\rightarrow` 2x+2 =1 or, 2x = 1-2 or, 2x = - 1 `\therefore` `x = \frac{-1}{2}` Thus given equation is true only for `x = \frac{-1}{2}`. This means calculated value of x satisfi

If A, B and C are single angles, then the angles of the form 2A, 2B, 2C, 3A, 3B, 3C etc., which are formed by multiplying the individual angle by integers like 2, 3, 4, ....., are called multiple angles. Relation of trigonometric ratios of multiple angles with those of single angles have major importance in various field of study such as physics, mathematics, engineering etc.  This post helps readers to learn about multiple angle formulae, derive these relations as well as apply these relations to solve few trigonometric problems. Some relations of multiple angles are given as below: sin2A =  2sinA. cosA = `\frac{2tanA}{1+tan^2A} =  \frac{2cotA}{cot^2A+1}` cos2A = `cos^2A - sin^2A = 2cos^2A-1 = 1-2sin^2A` cos2A = `\frac{1-tan^2A}{1+tan^2A} = \frac{cot^2A-1}{cot^2A+1}`  tan2A = `\frac{2tanA}{1-tan^2A}`   cot2A = `\frac{cot^2A-1}{2 cotA}`   sin3A = `3sinA - 4sin^3A`   etc. We try to prove these relations plus few other formulae as well on this post. 1. Proving the formula: sin2A = 2s

Being straight to the point: Suppose, A , B and C are  given angles. Then angles of the form A+B, A-B, A+B+C  and  A-B-C which are formed by addition or subtraction of two or more angles are called compound angles. The formula relating the compound angle with single angles is called compound angle formula. Trigonometric Compound Angle Formulae:  sin(A+B) = sinA cosB + sinB cosA sin(A-B) = sinA cosB - sinB cosA cos(A+B) = cosA cosB - sinA sinB  cos(A-B) = cosA cosB + sinA sinB tan(A+B) = `\frac{tanA+tanB}{1-tanA tanB}` tan(A-B) = `\frac{tanA-tanB}{1+tanA tanB}` cot(A+B) = `\frac{cotA cotB -1}{cotA + cotB}` cot(A-B) = `\frac{cotA cotB +1}{-cotA + cotB}` Proof of Compound angle Formulae: 1. Proving cos(A-B) = cosA cosB + sinA sinB Fig.1 Unit circle in X-Y plane to prove cos(A-B) = cosA cosB + sinA sinB. Consider a unit circle with its center at origin O(0,0) of X-Y co-ordinate system. Take two points P and Q on the circumference of the circle and join them to origin O, so that we