NEB grade 11 and 12 maths exam MCQ solved problems | NEB mathematics MCQ solved problems

-

 NEB  Mathematics grade 11 and 12 specification grid solutions

Short Solution Problems(Group A)


Rewrite the correct option in your answer sheet.

1. Which of the following is a statement?

a) The fishes are beautiful. b) Study Mathematics

c) x is the capital of country y. d) Water is essential for health.

Correct option: (d)

It because any sentence is considered as a statement if it is either true or false but not both. Among given options, (a), (b) and (c)  do not declare truth or falsity. But option (d) declares the truth that water is important for health.

2. The  value of: `\sqrt{-16} \times \sqrt{-25}` is, 

(a) -20 (b) -20i  (c) 20i  (d)20

Correct option: (a)

Here, 

`\sqrt{-16} \times \sqrt{-25}`

= `\sqrt{-1 \times 16} \times \sqrt{-1 \times 25}` 

But `i^2 = -1`, i = complex number.

= `\sqrt{i^2 \times 4^2} \times \sqrt{i^2 \times 5^2}`

= ` i \times 4 \times i \times 5`

= `i^2 \times 20`

= -20. //

Click here for NEB grade 11 maths short solution problems(Group A) 

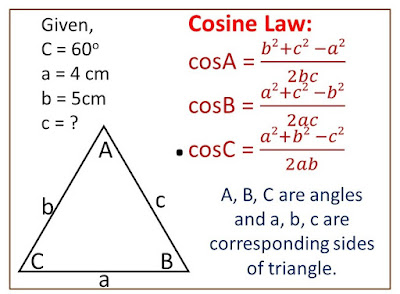
3.  If `\angle C = 60^o`, b =  5 cm and a = 4 cm of a `\triangle ABC`, then what is value of c ?

(a) 3.58 cm  (b) 4.58 cm  (c) 4.89 cm  (d) 4.56 cm

Correct option: (b)

Solution: By cosine law of triangle (`\triangle ABC`),    

`cosC = \frac{a^2 + b^2 - c^2}{2ab}`

or, `2ab cosC = a^2 + b^2 -c^2`

or, `c = \sqrt{a^2 + b^2 - 2ab cosC}`

or, `c = \sqrt{(4cm)^2 + (5cm)^2 - 2 \times 4cm \times 5cm \times cos60^o}`

or, `c = \sqrt{41 - 40 \times \frac{1}{2}}`

or, `c = \sqrt{41 - 20}`

or, c = 4.58 cm

`\therefore` c = 4.58 cm //

4. In a triangle ABC, `B = 120^o`, a = 1, c = 1, then other angles and sides are

(a) 35, 45, `\sqrt{2}`  (b)  10, 50, `\sqrt{3}` (c) 20, 40, 2  (d) 30, 30, `\sqrt{3}`

Correct option: (d)

Solution: By Cosine law,  


`cosB = \frac{c^2 + a^2 - b^2}{2ac}`

or, `b = \frac{c^2 + a^2 - 2ac cosB}`

or, `b = \frac{1^2 + 1^2 - 2.1.1.cos120^o}`

`\therefore` `b = \sqrt{3}`.

Also, Using sine law,

`\frac{a}{sinA} = \frac{b}{sinB} = \frac{c}{sinC}`

or, `\frac{1}{sinA} = \frac{\sqrt{3}}{sin120^o} = \frac{1}{sinC}`

Taking first and second ratios,

`\frac{1}{sinA} = \frac{\sqrt{3}}{sin120^o}`

or,  `sinA = \frac{sin120^o}{\sqrt{3}}`

or, `A = sin^-1(\frac{sin120^o}{\sqrt{3}})`

or,  `A = sin^-1(\frac{\frac{\sqrt{3}}{2}}{\sqrt{3}})`

or, `A = sin^-1(\frac{1}{2}) = 30^o`.

   `\therefore` `A = 30^o`

Again, taking second and third ratios,

`\frac{\sqrt{3}}{sin120^o} = \frac{1}{sinC}`

or, `C = sin^-1(\frac{sin120^o}{\sqrt{3}})`

`\therefore` `C = 30^o`.

Thus, required angles are `30^o, 30^o` and side is `\sqrt{3}`.//

5. The cosine of the angle between the vectors `\vec a = \vec i -2\vec j + 3\vec k` and `\vec b = \vec i + 3 \vec j + 3\vec k` is,

(a) `\frac{1}{14}` (b) 14  (c) `\sqrt{14}`  (d) 196.

Correct option: (c)

Soution:

    Cosine of angle  between vectors `\vec a` and `\vec b` is, 

`cos \theta = \frac{\vec a \cdot \vec b}{|\vec a| \cdot |\vec b|} .....(1)`

Here,

`\vec a \cdot \vec b = (\vec i - 2\vec j +3\vec k)\cdot (\vec i + 3\vec j + 3\vec k)`

                                = `\vec i \cdot \vec i - 2\vec j \cdot 3\vec j  + 3\vec k \cdot 3\veck`

`\therefore` `\vec a \cdot \vec b = 1 - 6 + 9 = 4`

Also, `|\vec a| = \sqrt{(1)^2 + (-2)^2 +(3)^2} = sqrt{14}`

and `|\vec b| = \sqrt{1^2 + 3^2 + 3^2} = \sqrt{19}`

Usin these values in (1)

`cos \theta = \frac{4}{\sqrt{14} \cdot \sqrt{19}} = \frac{4 \sqrt{14}}{14 \sqrt{19}}` 

                  = `\frac{2}{7 \sqrt{19}} \sqrt{14}`      

which is not exact as given in the options. But the possibility of the correct option is (c) because of similar factor `\sqrt{14}`. //

6. The equation of parabola with the vertex at the origin and the directrix y-2 = 0 is,

(a) `x^2 - 8y = 0` (b) `y^2 + 8y = 0` (c) `x^2 + 8y = 0`  (d)  `y^2 - 8y = 0`

Correct option: (c)

Solution:

A parabola is the locus or path of a point which lies at equal distance from it's focus and directrix. 

Here given directrix is 

y - 2 = 0 or y = 2. This means directric lies on positive y-axis. 

So, equation of parabola must be of the form,

`x^2 = 4ay ...(1)`

with focus at (0 , -a)

Since focus lies at equal distance from parabola as it's directrix, so -a =2. It is because directric passes through y-axis and focus also lies on y-axis. This means  focus (0 , -a) may also lie on the directrix.

Now using -a = 2, that is, a = -2 in (1),

`x^2 = 4ay = 4(-2)y = -8y`

`\therefore` `x^2 + 8y = 0` is required equation of the parabola, as shown in figure.//

7. A mathematical problem is given to three students Sumit, Sujan and Rakesh whose chance of solving it are `\frac{1}{2}, \frac{1}{3}` and `\frac{1}{a}` respectively.The probability that the problem is solved is `\frac{3}{4}`, the possible value of a are,

(a) `\frac{9}{2}` (b) 4 (c) `\frac{1}{4}`  (d) `\frac{1}{8}`

Correct option: (b)

Solution:-

Let's suppose the probability of Sumit, Sujan and Rakesh to solve problem be P(A), P(B) and P(C) respectively. Then

P(A) = `\frac{1}{2}`, P(B) = `\frac{1}{3}`,  P(C) = `\frac{1}{a}`

if 1- P(A) is probability that Sumit does not solve problem etc. then

probability that problem is solved = [1 - (1 -P(A)) (1 - P(B)) (1 - P(C))]

or, `\frac{3}{4} = [1 - (1- \frac{1}{2})(1 - \frac{1}{3})(1 - \frac{1}{a})]`

or, `\frac{3}{4} = [1 - (\frac{1}{2})(\frac{2}{3})(\frac{a - 1}{a})]`

or, `\frac{3}{4} = [1 - \frac{2(a-1)}{6a}]`

or, `\frac{2(a-1)}{6a} = 1 - \frac{3}{4} = \frac{1}{4}`

or, `2(a-1) = \frac{6a}{4}`

or, `a-1 = \frac{3a}{4}`

or, `a -\frac{3a}{4} = 1`

or, `\frac{a}{4} =1`

or, a = 4

`\therefore` a = 4 //

8. `\lim_(\theta->0) \frac{sin \theta}{\theta}` is equal to

(a) 0  (b) `\infty`  (c) 1  (d) `\frac{0}{0}`

Correct option: (c)

Solution:-

Using L-Hospitals rule,

`\lim_(\theta->0) \frac{sin \theta}{\theta}`

= `\lim_(\theta ->0) \frac{cos \theta}{1}`

= `coso` = 1.//

For NEB grade 12 physics numerical solutions: Visit Link 

9. The derivatives of `\frac{4x^2 + 3}{3x^2 - 2}` is 

(a)  `\frac{-34x}{(3x^2 - 2)^2}` (b)  `\frac{30x^2}{(3x^2 - 2)}`  (c)   `\frac{-32x}{(3x^2 - 2)^3}` (d)   `\frac{-31x}{(3x - 2)^2}`

Correct option: (a)

Solution:- Here,

`y = \frac{4x^2 + 3}{3x^2 -2}`

Using quotient rule of differentiation with respect to 'x',

`\frac{dy}{dx} = \frac{(3x^2 - 2) \frac{d}{dx}(4x^2 + 3) - (4x^2 + 3) \frac{d}{dx} (3x^2 - 2)}{(3x^2 - 2)^2}` 

or, `\frac{dy}{dx} = \frac{(3x^2 - 2) (8x) - (4x^2 + 3) (6x)}{(3x^2 - 2)^2}`

or, `\frac{dy}{dx} = \frac{24x^3 - 16x - 24x^3 - 18x}{(3x^2 - 2)^2}`

or, `\frac{dy}{dx} = \frac{-34x}{(3x^2 - 2)^2}`

`\therefore` `\frac{-34x}{(3x^2 - 2)^2}` is required derivative. //

10. By Newton's Raphson, the positive root of `x^3 -18 = 0` in (2, 3) is,

(a) 2.666 (b) 2.621  (c) 2.620  (d) 2.622

Correct option: (b)

Solution:-

Given, `f(x) =  x^3 -18 .....(1)`

If `x_1` is initial guess root of function f(x), then by Newton's Raphson method, second guess of root will be,

`x_2 = x_1 - \frac{f(x_1)}{f \prime (x_1)} .....(2)`

By direct method, you can gues root as

`x^3 - 18 = 0`

or, `x = (18)^{\frac{1}{3}} \approx 2.62`

so, let initial guess of root be, `x_1 = 2.62`

Taking derivative of (1)

`f \prime (x) = 3x^2`

or, `f \prime (2.62) = 3 \times (2.62)^2 = 20.5932`

Also, `f(2.62) = (2.62)^3 - 18 = -0.015272`

Using these values in (2),

`x_2 = 2.62 - \frac{-0.015272}{20.5932} = 2.62074... \approx 2.621`

`\therefore`  `x_2 = 2.621`, which is required root.//

11. Two forces acting at an angle of  `45^o` have a resultant equal to `\sqrt{10}` N, if one of the forces be `sqrt{2}` N, then what is the other force ?

(a) 1N (b) 2N  (c) 3N  (d) 4N

Correct option: (b)

Solution:-

The resultant force R between two forces `F_1` and `F_2` is given as

`R = \sqrt{(F_1)^2 + (F_2)^2 + 2F_1 F_2 cos \Theta } .....(1)` 

where `\Theta` is angle between two forces `F_1` and `F_2`.

By given,

`R =\sqrt{10}N`, `F_1  = \sqrt{2} N` and `\Theta = 45^o`, `F_2 = ?`

Using given values in (1),

` \sqrt{10} = \sqrt{(\sqrt{2})^2 + (F_2)^2 + 2\sqrt{2} F_2 cos45^o}`

or, `10 = 2 + F_2^2 + 2 \sqrt{2} \frac{1}{\sqrt{2}}`  

or, `8 = F_2^2 + 2F_2`

or, `F_2^2 + 2F_2 - 8 = 0`

or, `F_2^2 + 2F_2 +1 - 1 - 8 = 0`

or, `(F_2 + 1)^2 - 9 = 0`

or, `(F_2 + 1)^2 = 9`

or, `F_2 + 1 = \pm 3`

or, `F_2 = \pm 3 - 1`

Taking + sign, it is because angle between two forces is only `45^o`, this implies that these forcese are not antiparallel. So, `F_2` should have positive value. Taking - sign gives negative value of `F_2` which is not acceptable in this question.

`F_2 = + 3 - 1`

`\therefore` `F_2 = 2` N, which is required force. //

OR

The total cost function of a producer is given as `C = 500 + 30Q + \frac{1}{2}Q^2`. What is the marginal cost (MC) at Q = 4?

(a)Rs. 38 (b) Rs. 34 (c) Rs. 30  (d) Rs. 28

Correct option: (b)

Solution:- 

Given cost function is, `C = 500 + 30Q + \frac{1}{2}Q^2 .......(1)`

At Q = 4, marginal cost (MC) = ?

Marginal Cost is the ratio of change of total production cost of any quantity to change in that quantity.

That is, `MC = \frac{dC}{dQ}`

where dC is change in production cost and dQ is change in quantity.

Now differentiating (1) with respect to quantity(Q), we get

`\frac{dC}{dQ} = \frac{d}{dQ}(500+30Q+\frac{1}{2}Q^2)` 

 or, MC = 30 + Q

At  Q = 4,

`MC|_(Q=4) = 30 + 4 = 34`

Thus, the marginal cost is Rs. 34 //

Comments

Post a Comment

These posts may also be useful for you

top 3 websites for downloading research papers for free

-
  This post provides you valid links of top 3 websites from where you can download research papers published on high ranked journals for free. Just copy the Title or DOI of the papers, then go to either of these websites and paste on search bar and then hit search button.  1. Sci -hub  2. Library genesis 3.Core Download the file to get the links of these websites. Get File Doing research works is not only learning, it's innovation and interpretation of field of interest.  Watch video 👇👇 Watch Now Don't forget to Follow this blog.  Follow this Blog  
Read More »

plot graph in gnuplot from csv and data file | knowledge of physics

-
 If you are using LINUX based OS, for example Ubuntu, you must be familiar with plotting data in gnuplot saved in a file with .dat extension. It is very simple technique.  To plot data in .dat format, you simply go to gnuplot and run following command, gnuplot> plot 'file_name.dat' using 1:2  This command gives you simple plot of your data saved in  file_name.dat. You can further modify this plot by adding title, axes names, legends and colors of plot and width etc. Here 1:2 means first column of data is along x-axis and second column along y-axis. But what about if you have data in a file of  .csv format ? Let's discuss. CSV means coma separated variables. This means each column of the data in the .csv file is separated by coma (,), and gnuplot does not accept this format directly just as you do for the .dat file.  For gnuplot to read data from .csv file, you should tell it that data you are applying are in coma separated format. So, write code as below...
Read More »

projectile motion in fortran | relation of angle of projection and horizontal range

-
Image
 Have you ever tried to visualize projectile motion in fortran program? This post will help you to generate data and plot the graph of projectile motion.   Above figure shows you the angle of projection(°) versus horizontal range (meter) plot, where the speed of projection is 30 m/s. 👉 Click on link for NEB grade 12  physics numerical problem-solutions:-  LINK Let's start with some basic things: What is projectile and projectile motion ? Projectile:  A projectile is an object thrown to the sky with certain velocity against the earth's gravity. The motion that the projectile possesses during it's journey until it returns to the same surface, from where it was thrown, is called the projectile motion. In above figure, the projectile starts it's journey from point o and follows the curved path to reach another point on the same surface.  Suppose, `\theta` = angle of projection `\therefore` Angle of projection is the angle between the horizontal surface of ...
Read More »

NEB physics exam numerical problems with solutions for grade 12 students

-
Image
 This post provides you the numerical problems and their solutions of physics based on NEB(National Examination Board) syllabus grade 12. Solutions of Previously Asked Numerical Problems in NEB exams. Q.1. A coil consisting of 100 circular loops with radius 0.60 cm carries a current of 5A. At what distance from the center, along the axis, the magnetic field has magnitude as `\frac{1}{8}` great as it is at the center? Solution:- Given, number of circular loops = N = 100 radius of the loop, `r = 0.60cm = 6.0 \times 10^-3` m. current, I = 5 A Magnetic field at the center of loop = B (suppose) magnetic field at distance x from the center = `\frac{1}{8}B`   To find, x = ? The magnetic field at distance x from center of the coil is given as, `B = \frac{\mu_o I N r^2}{2(x^2  + r^2)^(\frac{3}{2})}`. By given in question, magnetic field at x = `\frac{1}{8} \times` magnetic field at x = 0.       or, `\frac{\mu_o I N r^2}{2(x^2 + r^2)^(\frac{3}{2})} =\frac{1...
Read More »

how to plot 3D and parametric graphs in gnuplot | three dimensional plot in gnuplot software

-
Image
Although being an open-source plotting software, gnuplot gives you almost all feasibilities to plot 2D, 3D, parametric plots and even the gif as well as animations.  Here you can learn to plot three dimensional graphs in gnuplot. Additionally, you also get the idea of parametric plots in gnuplot software. 1. 3D graphs in gnuplot To plot 3D graphs you just need to replace the command 'plot' for 2D graphs by 'splot' for 3D graphs.  Here, splot means surface plot.  Plotting graphs in 3D view allows you to observe it from all possible sides of the graph.  You rotate it upward, downward , left-side as well as to right-side.  Example: gnuplot >  splot sin(x) Then press ENTER key. You get the output as it looks as picture below: Fig. 1 3D graph of sin(x). 2. parametric plots Parametric plots can be created both in 2D and 3D.  For 2D graph, the dummy variable is t, whereas for 3D plot, they are u and v. Example: Image of parametric plot is shown below: Fig....
Read More »

how to create GIF animation in gnuplot | animation using gnuplot software

-
Image
 GNUPLOT software is not only 2D and/or 3D plotting tool, but it also provides flexibility to create animation and GIF animation plots.  GIF means Graphics Interchange Format. It is a repeated display of images from same of different sides. It helps you to view the image clearly so that you don't need to pay much attention to understand it.  This post provides you tools and techniques to create GIF animation in gnuplot. Codes necessary for creating the GIF are given in links. Please check it as well. GIF can also be both 2D and 3D.  You must use 'plot' command to create 2D GIF and 'splot' command to create 3D GIF. 👉 To learn to create plots in gnuplot: Click Here   👉 To learn gnuplot basics for beginners: Click Here Example of 2D GIF: GNUPLOT code for creating above GIF, 👇 gnuplot > set title 'gif image of sine and cosine functions' gnuplot > set xlabel 'x' gnuplot > set ylabel 'sine and cosine' gnuplot > f1(x,t) = sin(x-t) gnu...
Read More »

NEB board exam maths solved problems with proper solutions - available for free | short answered mathematics problems solved group A

-
Image
 This post provides you the problems with solutions of NEB board exam of grade 11 mathematics 2076. Attempt All Questions. Group A  `5 \times 3 \times 2 = 30` Get full question paper from Here . 1. a. Find the truth value of the biconditional statements of p and q where p represents '2 is an even number' and q represents '4 is an even number'. Solution:- Biconditional statements imply if one statement is true then another is also true. if one is false, then another statement is also false. So, one statement supports the other in case of biconditional statement.  Here, p: 2 is an even number.          q: 4 is an even number. 4 is the square of 2 and 2 is the square root of 4. 2 is even, then 4 is also even. So, both p and q represent true value (T). p q p ⇔ q T T T Thus truth value of p and q is T, i.e. 2 is an even number implies 4 is also an...
Read More »