proof of limit of sinθ/θ as θ tends to 0

 In this post, you will learn to prove a very important formula in calculus, 

`\lim_{\theta \rightarrow 0} \frac{sin \theta }{\theta} = 1`.

This relation is very useful in determining the limit of trigonometric functions. 

If you use `\theta = 0` directly in `\frac{sin \theta}{\theta}` then you get `\frac{0}{0}` which is an indeterminate form. This means that you can not find value of limit directly. However, if you use some techniques, then you get the limit equal to 1. In this post, you will learn that technique which helps you to find out the value of given limit easily.  

Let's begin.

Fig.1 Circle with center at C having radius CB = r and tangent MN at point M to prove the formula.

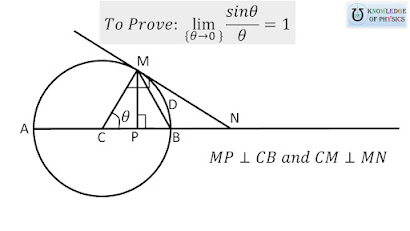
Consider a circle ABDM with center at C and radius CB so that 

CM = CB = AC = r.

BDM  is an arc that subtends angle `\theta` at C. 

MN is a tangent of circle at M that meets diameter AB extended at N so that CM is perpendicular to MN. Also, MP is drawn to perpendicular to CB at P. 

Now we consider two right angled triangles `\triangle CBM` and `\triangle CMN `. We also consider a sector CBDM of circle, so that 

`\text{Area of}\triangle CBM \leq \text{Area of sector CBDM} \leq \text{Area of } \triangle CMN ` ----(1)

Now,

To find out Area of `\triangle CBM`:

In right triangle triangle CBM, 

Area of `\triangle CBM = \frac{1}{2} \text{Base} \times \text{Height}`

or, Area of `\triangle CBM  = \frac{1}{2} CB \times PM`

We  know, CB = r and `\angle BCM = \theta`, so that 

`sin\theta = \frac{PM}{CM} = \frac{PM}{r}`

`\therefore` `PM = r sin\theta`, which gives,

Area of `\triangle CBM = \frac{1}{2} r \times r sin\theta`

`\therefore` Area of `\triangle CBM = \frac{1}{2} r^2 sin \theta` ----(2)

To find out Area of Sector CBDM:

 The process of finding the area of sector CBDM is little bit different than finding the area of triangles. 

Suppose  A' is area of Sector CBDM. 

We have from above figure, 

Area of circle of radius r is `\pi r^2`.

This circle of area `\pi r^2` makes angle `2\pi` at the center C. 

The portion CBDM with arc `\overarc {BDM}` makes angle `\theta` at the center C.

Thus, angle `2\pi` is equivalent to area `\pi r^2`.

and angle `\theta` is equivalent to area A'.

And you see that bigger angle corresponds to larger area. Thus, the area and the angle are in proportional.  That is,

`\frac{A'}{\pi r^2} = \frac{\theta}{2 \pi}`

or, `A' = frac{\theta}{2 \pi} \pi r^2`

`\therefore` `A' = \frac{1}{2} r^2 \theta` ----(3)

This gives area of sector CBDM of circle.

To find out Area of `\triangle CMN`:

In right angle triangle CMN, 

CM = r and `\angle MCN = \theta`.

MN = ?

Area of `\triangle CMN = \frac{1}{2} \text{Base} \times \text{Height} `

or, Area of `\triangle CMN = \frac{1}{2} CM \times MN`

From figure,

`tan \theta = \frac{MN}{CM}`

or, `\tan \theta = \frac{MN}{r}`

`\therefore` `MN = r tan\theta`, so that

Area of `\triangle CMN = \frac{1}{2} r \times r tan\theta`

`\therefore` Area of  `\triangle CMN = \frac{1}{2} r^2 tan\theta` -----(4)

Now, Finding out the Limit:

  Using equation (2), (3) and (4) in (1), we get

`\text{Area of}\triangle CBM \leq \text{Area of sector CBDM} \leq \text{Area of } \triangle CMN `

`\implies \frac{1}{2} r^2 sin\theta \leq \frac{1}{2} r^2 \theta \leq \frac{1}{2} r^2 tan\theta`

The factor `\frac{1}{2} r^2` being same in all sides, cancels out.

`\implies  sin\theta \leq \theta \leq  tan\theta` 

`\implies sin\theta \leq \theta \leq \frac{sin\theta}{cos\theta}`

Dividing by `sin\theta` in all sides,

`\implies 1 \leq \frac{\theta}{sin\theta} \leq \frac{1}{cos\theta}`

Taking reciprocal of all sides, the symbol 'Less than or equal to (`\leq`)' changes to the symbol  'Greater than or equal to (`\ge`)'. That is 

`\implies 1 \ge \frac{sin\theta}{\theta} \ge cos\theta`

Now taking limit as `\lim_{\theta \rightarrow 0}` in all sides, 

`\implies \lim_{\theta \rightarrow 0} 1 \ge \lim_{\theta \rightarrow 0} \frac{sin \theta}{\theta} \ge \lim_{\theta \rightarrow 0} cos \theta`

But `\lim_{\theta \rightarrow 0} cos \theta = 1` and `\lim_{\theta \rightarrow 0} 1 = 1`, so

`\implies  1 \ge \lim_{\theta \rightarrow 0} \frac{sin \theta}{\theta} \ge 1`

Here, we got an amazing form of inequality, which says that `\lim_{\theta \rightarrow 0} \frac{sin \theta}{\theta}` is both less than or equal to 1 and greater or equal to 1. Which is possible only if,

`\lim_{\theta \rightarrow 0} \frac{sin \theta}{\theta} = 1`. This proves the relation.

This relation says that as `\theta` measured in radian unit, (not in degree) approaches to 0 radian, the value of `\frac{sin \theta}{\theta}` approaches to 1. However, if you directly put `\theta = 0` in `\frac{sin \theta}{\theta}`, it gives `\frac{0}{0}` which is an indeterminate form.  

Note:

This result is very important in calculus for finding out the limit and derivatives of trigonometric functions, such as sin x, cos x, tan x etc.

For video explanation: CLICK HERE.

Share this post with others if you found it useful.